Якщо R-статистика не встановлена, то завантажити її з сайту r-project.org та встановити. Можна завантажити та встановити R-Studio або використати її веб-версію)*.

Базова статистика в R

Завдання

Для даної вибірки розрахувати наступні характеристики: середнє значення, вибіркову дисперсію, стандартне відхилення, медіану, довірчі інтервали для середнього та дисперсії.

Виконання

Введення даних:

Масив даних=c(Список значень)

Середнє значення:

$$\bar{X}=\frac{1}{n}\sum\limits_{i=1}^n {x_i}$$

Функція для розрахунку:

mean(Масив даних)

Вибіркова дисперсія:

$$s^2=\frac{1}{n-1}\sum\limits_{i=1}^n( x_i-\bar{x})^2$$

Функція для розрахунку:

var(Масив даних)

Вибіркове стандартне відхилення:

$$s=\sqrt{s^2}$$

Функція для розрахунку:

sd(Масив даних)

Медіана. :

Функція для розрахунку:

median(Масив даних)

Розрахунок меж довірчого інтервалу для математичного очікування (середнього):

$$M_{min}=\bar{x}-\frac{t_{\alpha, n-1} \cdot s}{\sqrt{n}}$$

$$M_{min}=\bar{x}+\frac{t_{\alpha, n-1} \cdot s}{\sqrt{n}}$$

\(t_ {\alpha, n-1}\) — коефіцієнт розподілу Стьюдента з рівнем недостовірності α (звичайно вживають величину 5% (0.05), n-1 — кількість ступенів свободи, для звичайної виборки на одиницю менше кількості чисел у виборці.

Функція для розрахунку коефіцієнта Стьюдента*:

qt(1-α/2,n-1)

*В функції qt із-за недостатьої проробки програми використовується значення ймовірності 1-α/2 замість 1-α . (Чисельно двохстроннє t_1-α/2,n-1 рівне односторонньому t_1-α.n-1)

Розрахунок меж довірчого інтервалу для дисперсії:

$$\sigma_{max}=\frac{(n-1) \cdot s^2}{\chi^2_{\alpha/2,n-1}}$$

 $$\sigma_{min}=\frac{(n-1) \cdot s^2}{\chi^2_{1-\alpha/2,n-1}}$$

\(\chi^2_{1-\alpha/2,n-1}\) і \(\chi^2_{\alpha/2,n-1}\) — коефіцієнти розподілу χ² з відповідними рівнями недостовірності та кількістю степеней свободи.

Функція для розрахунку коефіцієнта χ²:

qchisq(довірчий рівень,n-1)

Візуальне представлення результатів розрахунку

Побудова діаграми розмаху:

Функція для розрахунку:

boxplot(Масив даних)

Середнє значення на діаграмі:

abline(h=mean(Масив даних),col="Колір")

Межі довірчого інтервала на діаграмі:

abline(h=c(M_min,M_max),col="Колір")

Завдання для самопідготовки

Для кожної вибірки розрахувати характеристики, розрахувати межі довірчих інтервалив для середього та дисперсії, побудувати діаграми розмаху.

1. x = 11, 12, 11, 13, 15;
2. y = 43, 41, 42, 45;
3. z = 22.5, 22.8, 22.7, 22.6, 22.8, 22.1.

Додаткові матеріали по темі

https://r-analytics.blogspot.com/2018/04/blog-post_28.html

http://stat.org.ua/statclasses/descriptive-statistics/

Порівняльні експерименти

Завдання

Дано дві виборки. Потрібно визначити, чи є між ними статистична різниця за допомогою t-тесту..

Інструкції

При парних випробуваннях можливі три принципово різні випадки:

а) порівняння двох виборок з однаковими дисперсіями;

б) порівняння двох виборок з різними дисперсіями;

в) парні спостереження (з холостим дослідом).

1. Перевірка на рівність дисперсій

 Якщо у нас не явний випадок парних спостережень (випадок «в»), то спочатку треба перевірити гіпотезу про рівність дисперсій двох серій вимірювань. Нехай в нас є дві серії вимірювань:  і  — відповідно n замірів величини X та m замірів величини Y.

Розраховуємо , , ,  (лабораторна робота № 1, стор.3).

Гіпотеза про рівність дисперсій перевіряється за допомогою F-тесту, для цього розраховується F-статистика:

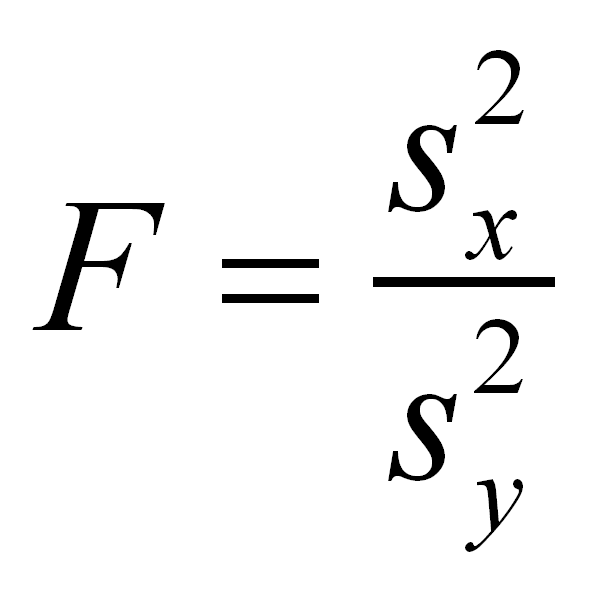 (більша дисперсія ділиться на меншу!)

Якщо    то статистично дисперсії X та Y рівні

Якщо , то статистично дисперсії X та Y відрізняються

 — коефіцієнт F-розподілу (F-критичне), $$\alpha$$  — рівень недостовірності,. β — кількість ступенів свободи виборки з більшою дисперсією, γ — кількість ступенів свободи виборки з меншою дисперсією. Кількість ступенів свободи на один менше ніж кількість вимірювань відповідної величини. Якщо , то виборки формально міняються місцями.

Розрахунок за допомогою R-статистики:

Функція для проведення F-тесту:

var.test(x,y)

Дисперсія x повинна бути більшою ніж y.

Функція для розрахунку коефіцієнта F-розподілу: 

qf(0.95,dfx,dfy)

Дисперсія x повинна бути більшою ніж y.

2. Випадок статистичної рівності дисперсій

Якщо дисперсії рівні, то наявність статистичної різниці виявляється наступними чином:

Перевірочна t-статистика визначається формулою:

$$t_{\nu}=\frac{|\bar{x}-\bar{y}|\cdot\sqrt{n+m-2}}{\sqrt{\frac{1}{n}+\frac{1}{m}}\cdot\sqrt{(n-1)\cdot s_x^2+(m-1)\cdot s_y^2}}$$

 — кількість ступенів свободи;

 порівнюється з відповідним коефіцієнтом Стьюдента  (t-критичне) з рівнем недостовірності ймовірності α, та кількістю ступенів свободи \(\nu\).

Якщо , то між серіями вимірювань є статистична різниця;

Якщо , то між серіями вимірювань немає статистичної різниці.

Розрахунок за допомогою R-статистики:

Функція для проведення t-тесту:

t.test(x,y,var.equal=TRUE)

Дисперсія x повинна бути більшою ніж y.

Функція для розрахунку коефіцієнта t-розподілу: 

qt(0.975,df)

df визначаєтся в результаті t-тесту.

3. Випадок статистичної нерівності дисперсій

Якщо дисперсії різні, то наявність статистичної різниці виявляється наступними чином:

Перевірочна статистика визначається формулою:

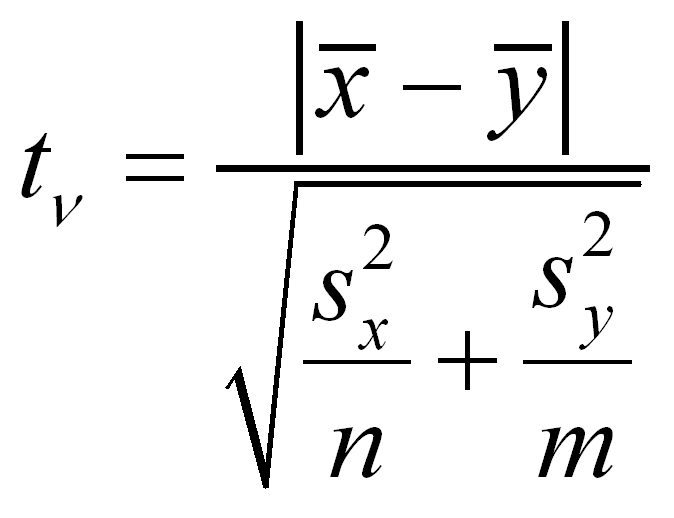
кількість ступенів свободи:

$$\nu=\left[\frac{\left(\frac{s_x^2}{n}+\frac{s_y^2}{n}\right)^2}{\frac{1}{n-1}\cdot\left(\frac{s_x^2}{n}\right)^2+\frac{1}{m-1}\cdot\left(\frac{s_y^2}{m}\right)^2}-2\right]$$

 порівнюється з відповідним коефіцієнтом Стьюдента  (t‑критичне) з рівнем недостовірності α, та кількістю ступенів свободи ν.

Якщо , то між серіями вимірювань є статистична різниця;

Якщо , то між серіями вимірювань немає статистичної різниці.

Розрахунок за допомогою R-статистики:

Функція для проведення t-тесту:

t.test(x,y,var.equal=FALSE)

Дисперсія x повинна бути більшою ніж y.

Функція для розрахунку коефіцієнта t-розподілу: 

qt(0.975,df)

df визначаєтся в результаті t-тесту.

4. Порівняння з холостим дослідом

Третій випадок відрізняється від попередніх тим, що тут дисперсія апріорі однакова й немає сенсу її перевіряти.

Перевірочна статистика визначається формулою:

$$t_{n-1}=\frac{\bar{d}}{s_d}\cdot\sqrt{n}$$

де  — середнє значень ,  — стандартне відхилення .

 порівнюється з відповідним коефіцієнтом Стьюдента  (t‑критичне) з рівнем недостовірності , та кількістю ступенів свободи n-1.

Якщо , то між серіями вимірювань є статистична різниця;

Якщо , то між серіями вимірювань немає статистичної різниці.

Розрахунок за допомогою R-статистики:

Функція для проведення t-тесту:

t.test(x,y,paired=TRUE)

Функція для розрахунку коефіцієнта t-розподілу: 

qt(0.975,df)

df визначаєтся в результаті t-тесту.

Візуальне порівняння*

boxplot(x,y)

 Звдання

Варіант № 1

1. Визначити, чи є різниця між двома виборками:

Варіант № 2

1. Визначити, чи є різниця між двома виборками. Парні дослідження:

Варіант № 3

1. Визначити, чи є різниця між двома виборками:

В якості відповіді на завдання відправте лог виконання команд в R-статистиці

*Спробуйте визначити, чи є різниця між виборками на око, аналізуючи діаграму розмаху. Порівняйте з висновком, зробленим на основі розрахунку ;)